manacher介绍及图文讲解（用于求解最长回文子串）

manacher算法是一种可以在O(N)时间复杂度下求字符串所有回文子串的算法，也是求最大回文子串最高效的算法。这种算法在进行遍历的时候，充分利用了回文串的特性，减少了许多不必要的计算，使得时间复杂度降低到了线性水平。该算法的难度在于理解，一旦理解后，代码是非常简单的。

manacher算法有如下几个要点：

• 如何计算回文串长度（O($N^2$)算法）
• 如何将奇回文串与偶回文串统一判断
• 如何优化O($N^2$)时间复杂度的中心拓展算法
  下面我们来一一讲解

一、如何计算回文串长度

如果没有时间上的限制，我们可以使用暴力的做法：中心拓展法

我们知道，如果一个字符串是回文串，那么该字符串必是中心对称的。故我们可以选择一个中心，从它开始，向两边逐一判断字符是否相同，拓展回文串长度。由于回文串可以是奇回文串也可以是偶回文串，我们需要选择一个字符或者选择两个字符中间作为中心进行逐一判断，故一共有 N + N - 1个中心。

二、奇回文串与偶回文串的统一判断

回文串既可以有aba的形式，也可以有abba的形式，在实际写代码的时候如果不进行处理，会使得代码变得比较复杂。
因此我们可以在每两个字符间及字符串头、尾加上一个不曾在字符串中出现过的字符，如#、$等字符，使得在进行遍历的时候可以不用分情况讨论

例如：

则我们可以对所有字符做中心拓展，得回文半径Pi，则原字符串的子回文串长度为Pi - 1
代码如下:

1
2
3
4
5
6
7

void mid(string s){
    int P[105];
    for(int i = 0;i<s.size();i++){
        P[i] = 1;
        while(s[i+P[i]]==s[i-P[i]]) P[i]++;		//P[i]为回文半径，故i±P[i]为需要进行拓展的最外层
    }
}

三、中心拓展算法的优化：manacher算法

目前我们已经有了时间复杂度为O($N^2$)的算法，如何优化呢。

不难发现，回文串的特点为中心对称，也就是说在回文串当中，围绕对称中心，左半边与右半边是完全相同的。故一个在左半边回文串内的子回文串，也必定存在于右半边，如该字符串
以b为对称中心，左边aba的子回文串在右边也出现了，那么我们可以思考一下，如果以从左到右的顺序进行中心拓展遍历，是不是可以通过已经计算过的回文半径来给当前还未计算的回文半径进行赋值？答案是显然的，但我们还需要考虑几种不同的情况。

我们知道上述理论成立的基础，是建立在回文串左右对称的前提下的，也就是说，我们如果想把过去计算过的回文半径拿来用，必然需要判断一下子回文串是否包含在大回文串之内，也就是如下三种情况：

• 当前中心在回文串的对称位置下的子回文串在回文串内
  这是最简单的情况也是我们最希望看到的情况，因为我们可以直接使用已经计算过的回文半径来进行赋值
  
  如我们遍历到当前位置时（绿色箭头），可以通过已经计算过的对称位置子回文串对称中心（橙色箭头）得到当前回文半径，也就是1。

• 当前中心在回文串的对称位置下的子回文串超出了回文串的范围
  如果对称位置下的子回文串并不完全被包含在回文串内，这种情况下不能直接将对称位置的回文半径赋值。但由于回文串的性质，我们可以保证包含在回文串内部的子串一定是回文串，则该种情况下当前位置的回文半径就是当前位置到回文串边缘的距离。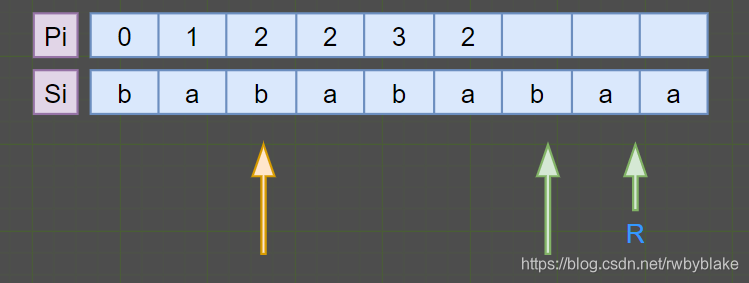
  
  当前我们计算到绿色箭头时，对称位置的Pi = 2，但当前位置距离最大回文串的边界只有1，则只能将其赋值为1。

• 当前中心已经不在回文串范围之内了
  这种情况下，一切都是未知的，只能用中心拓展算法来进行计算，也就是将该中心初始化为1，并进行中心拓展算法。

四、代码实现

虽然上面啰里啰嗦讲了一大堆，但实际代码非常简单，可以说理解了之后不用记模板随便敲的那种。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

string s, str;          //s为原字符串，str为添加字符后的字符串
int P[N];               //保存每个字符的回文半径
void add() {
    str+='^';
    for (int i = 0; i < s.size(); i++) {
        str += '#';
        str += s[i];
    }
    str+='#';
    str+='@';
}

void manacher() {
    int R = 0, mid = 0;
    for (int i = 1; i < str.size() - 1; i++) {
        P[i] = R > i ? min(P[2 * mid - i], R - i) : 1;	//进行三种情况的判断
        while (str[i + P[i]] == str[i - P[i]]) P[i]++;	//中心拓展
        if (i + P[i] > R) {                           	//如果当前回文串已经覆盖到了原先没有覆盖到的地方，则更新标记
            R = i + P[i];
            mid = i;
        }
    }

最后放一道模板题
最长回文